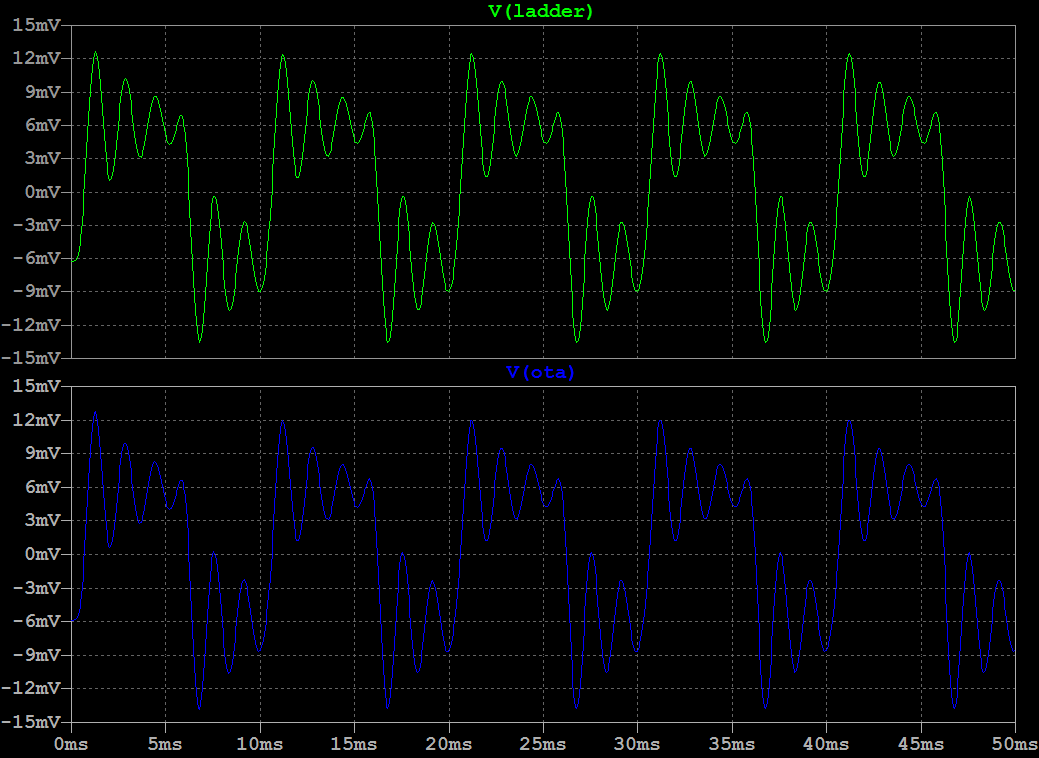
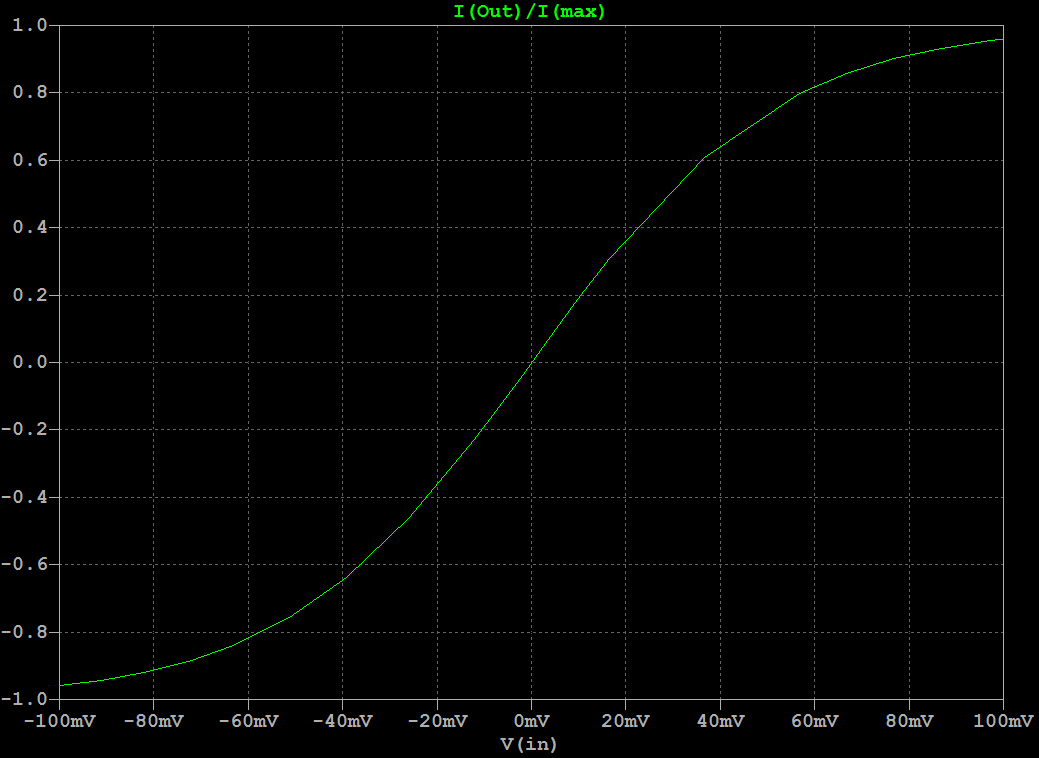
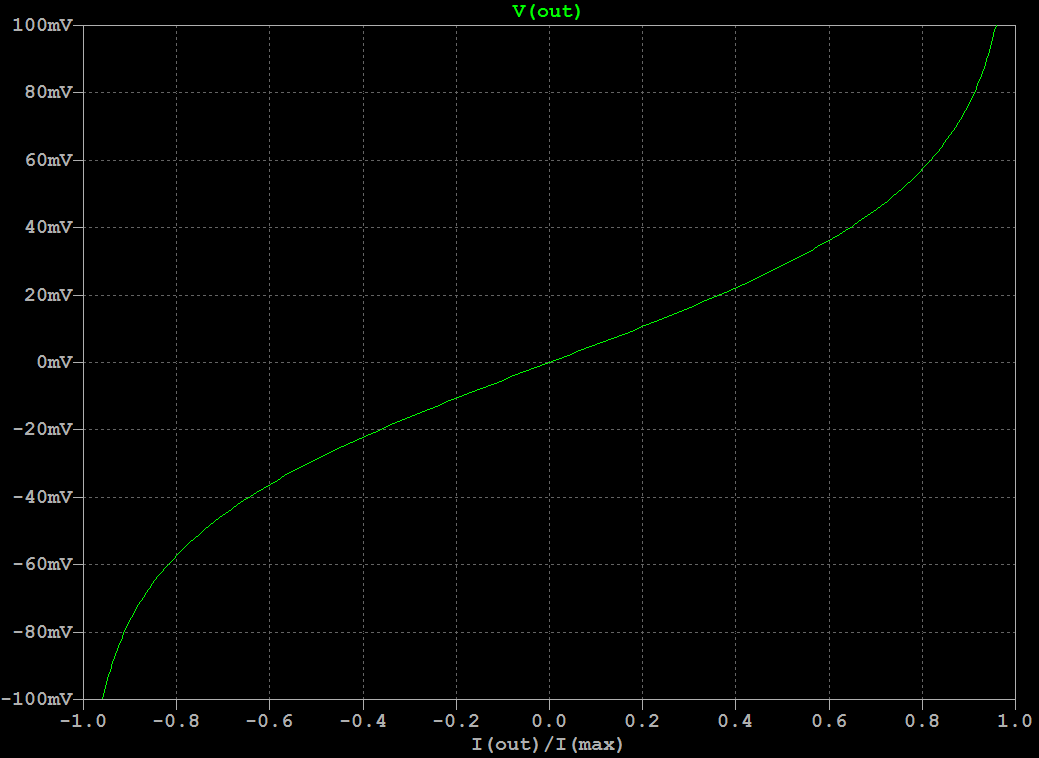
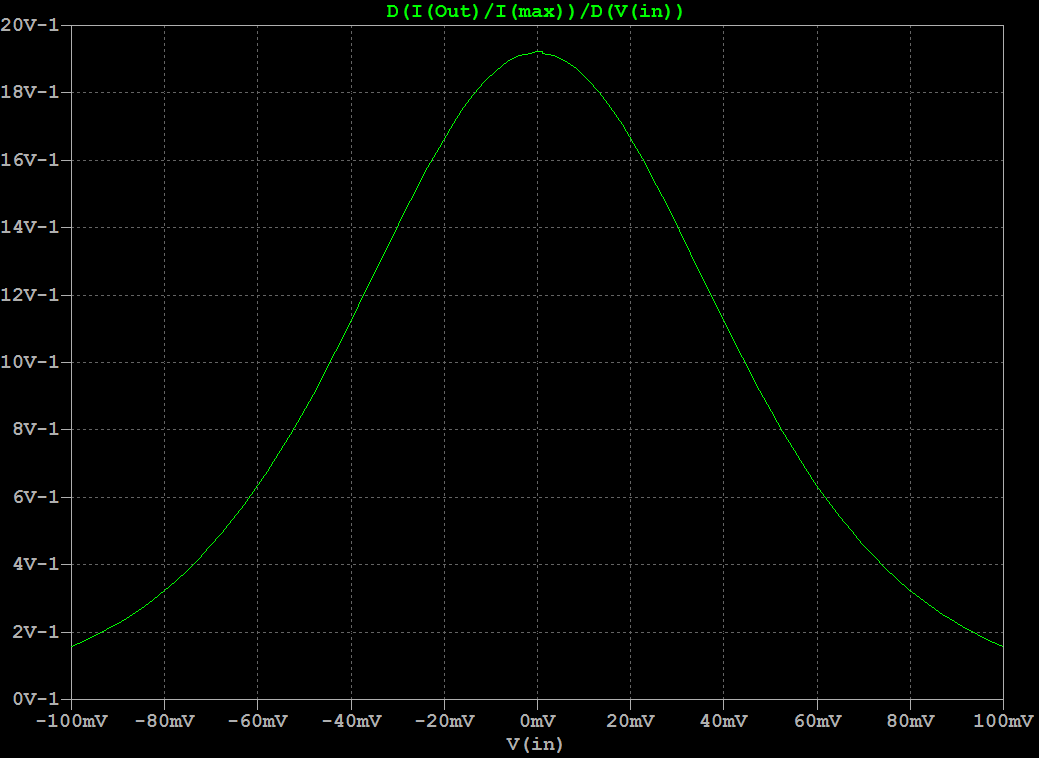
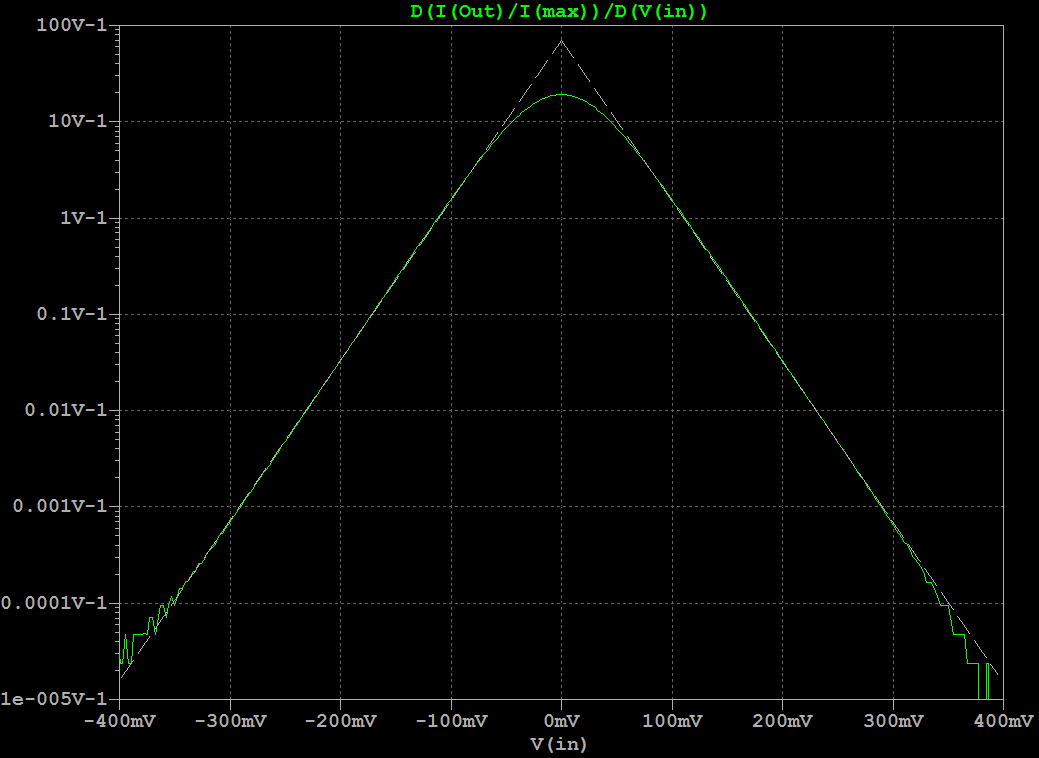
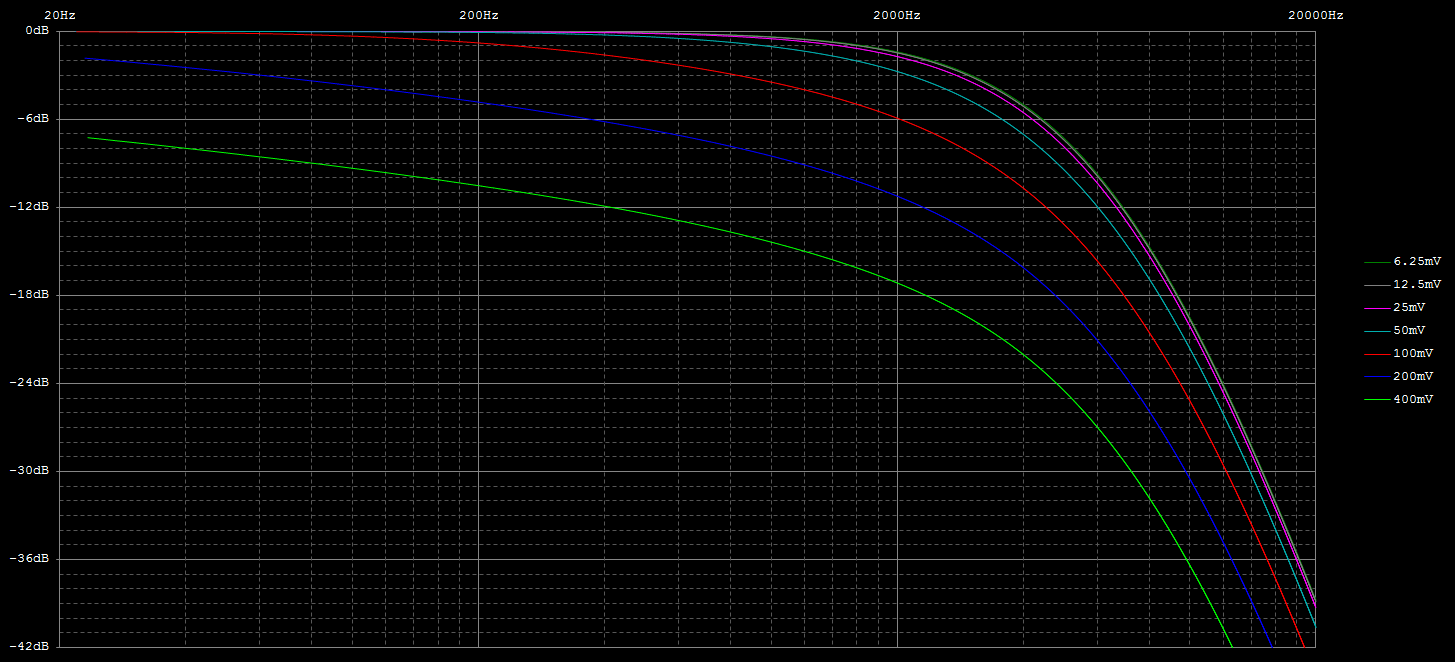
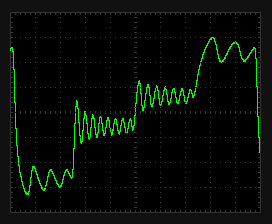
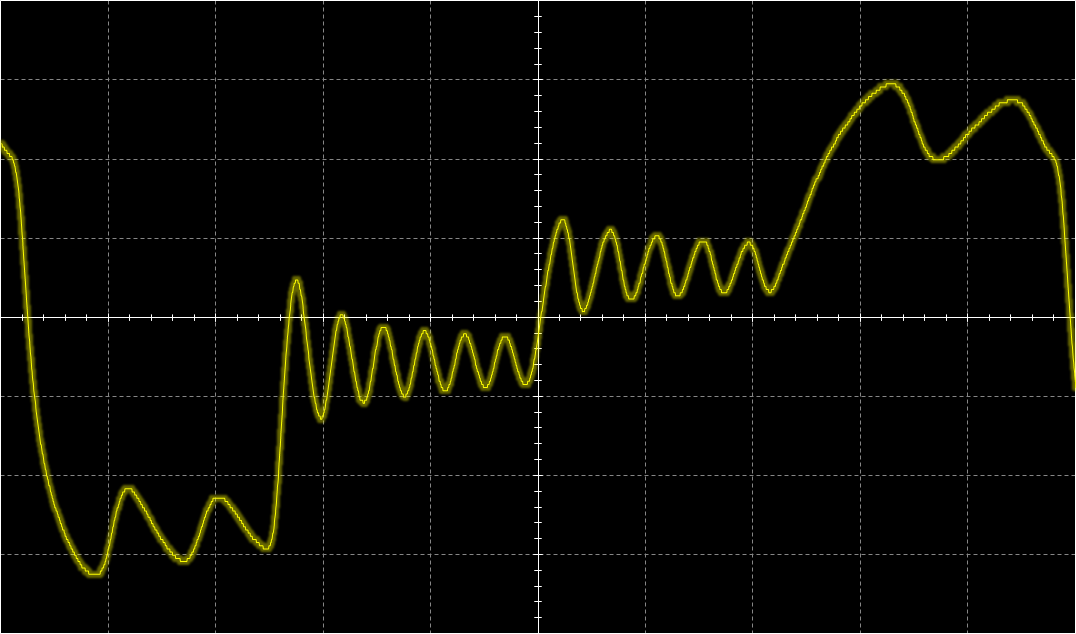
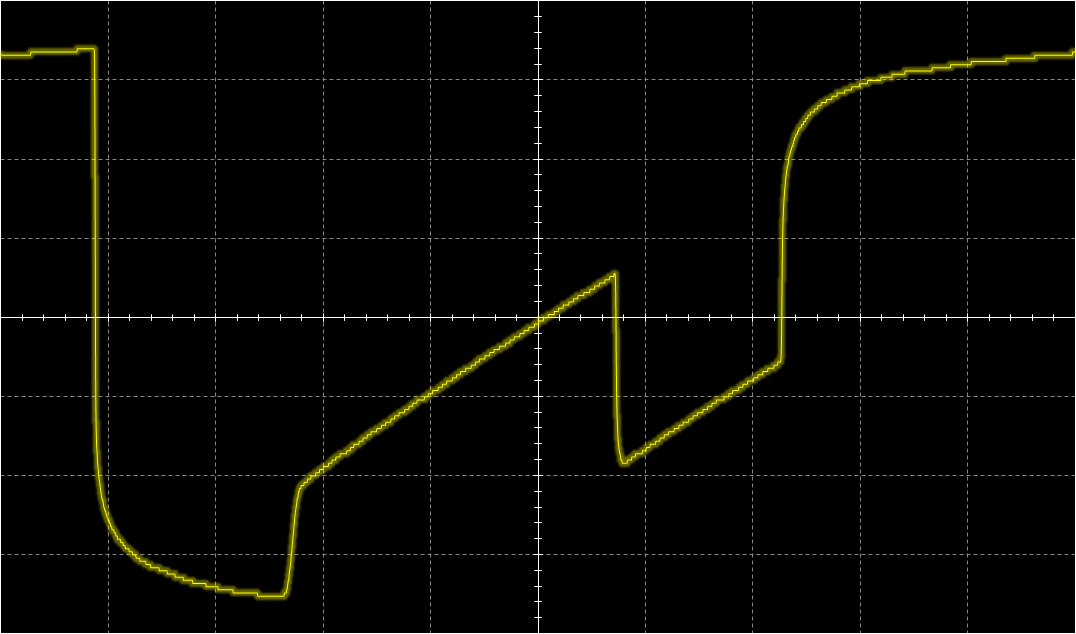
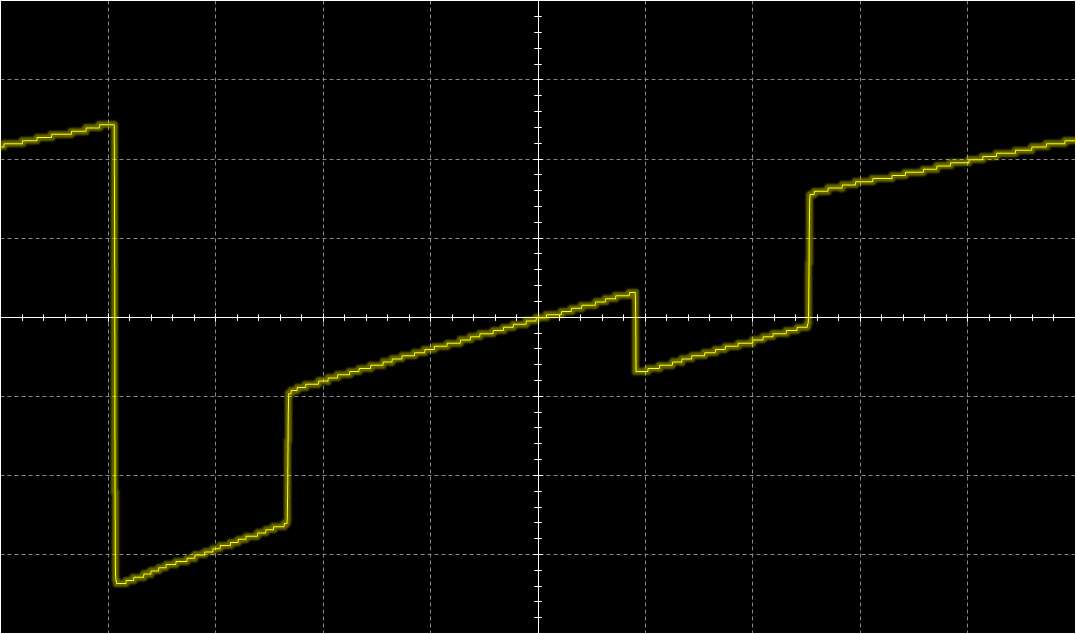
IntroductionThis is a new VCF/VCA combo that replaces the original 80017A hybrid modules in a Juno-106 (or any other synth that uses these). It gives the Juno-106 a much bigger sound without sacrificing the original 80017A's precision which makes the juno-106 sound so good polyphonically. The Juno-106 has a lot going for it: Complete hands-on control with one button or fader per parameter, complete midi control for each parameter through SysEx, ultra-stable DCOís, thundering bass-boost with the HPF in its lowest position and the above mentioned precision of the VCF. This precision comes in the form of excellent frequency tracking and a very flat resonance response. The former, not only allows playing notes by using the self-oscillating filters as extra oscillators, but also allows several of them to slowly beat against each other, even when separated several octaves apart. The later allows this beating to go really deep and is also fundamental in getting everything summed together without clipping. After all 24 waveforms (Saw, Tri, Sub and Sine, from self-oscillation, multiplied by 6 voices) have to be summed together with chorus on top. However, this precision comes in part from the filter being virtually distortion-free and this comes at the cost of its sonic character. Or actually, its lack thereof. And, to my taste, itís a bit too clean and bright, certainly taking into account that there is only one oscillator per voice. So, I wanted to give the filter a bit more character, let it add some harmonics and move things a bit to the lower regions of the spectrum. I would describe this as a kind of growling quality. Sound SamplesHere are 2 short samples of the prototypes, quickly recorded straight from the Juno-106 with the onboard sound chip of my laptop. No extra effects or post-processing were done on them.Note that the sweeping noise comes from the Juno's own chorus and that some glitches are present due to my laptop being overloaded with measurement software running at that time. Prototype Demo 1 Prototype Demo 2 Technical DetailsFirst of all I did not want to take things too far, it still had to be recognizable as juno-106, not something messed up beyond recognition. So, the filter had to be a 4-pole low-pass filter with all its poles in the real domain and as I consider the Juno-106 a bass-monster its resonance had to have Q-compensation. As this kind of filterís sonic character can be entirely defined by the dynamic position of its poles, its non-linearities and where these happen, it is interesting when these parameters are adjustable. Problem is, that by design, the Juno-106 has few adjustable parameters and for example, gradually distorting the filter by increasing its input level is not possible here as its waveforms are on/off (except for the sub). Adding extra controls for this purpose and making them, like the others, programmable and midi-controllable would be a project of an entirely different magnitude and doing this non-adjustable would mean for it to be impossible to play the pure undistorted waveforms. To accommodate all this I used a highly modified ladder filter. Its design originates from experiments I did about 2 decades ago with the intention of improving the original 1960ís Moog design. My main beef with it was that it is quite noisy, has low PSRR, and has little headroom: the onset of distortion (1% THD) happens at about 25mV input signal amplitude and it clips (90% of maximum amplitude reached) at only 75mV. Also, resonance disappears at low frequencies and increases a lot at high frequencies. Noise was reduced by getting rid of all external base resistances: the differential inputs were sourced by low-output-Z buffers and the bias resistors for the ladder were replaced with a stack of bandgap references, the top one also cured the low PSRR. Headroom was increased by replacing the open-loop differential output amplifier, which also serves as resonance amplifier, with a high-Z instrumentation amplifier that stays linear to almost full-rail signals. Changing the whole structure to a DC-coupled one, by getting rid of all coupling capacitors and mirroring the exponential converter so that the differential input pair accepts ground-referenced signals, together with the increased impedance of the output/resonance amplifier cured the low frequency limit, so that it can operate and self-oscillate down to the miliHertz range. HF resonance issues were solved by phase-compensating the loop-delay. My unwary expectation of this improved design, based on the assumption (and popular belief) that most of the magic happens in the ladder, was for its sonic character to be unaltered, but then without the noise and with a much bigger bottom-end. Much to my surprise it sounded entirely different, ultra-clean actually. Something I would rather expect from closed loop OTA based filters than from an open-loop ladder filter. When doing a Side-by-side comparison of this design with an OTA based 4-pole LPF, both tuned to the same frequency and resonance feedback, I had a very hard time to discern any difference between them. When feeding them sawtooths and squarewaves, I actually couldnít hear any difference. This was also confirmed by simulations. This lack of distortion comes from the last 2 (matched pair) transistors in the ladder that act as an error corrector. The input stage (also a matched pair) of the ladder converts the differential input voltage into differential current in a non-linear (see plot below) way. These last 2 transistors do the opposite: they convert this differential current back into a differential voltage across the last filter capacitor. This time with a non-linear relationship thatís the inverse of the input stageís non-linearities. So, as long as these are matched, errors are corrected and distortion remains absent. Note that the other transistors in the ladder have no influence. They just serve as cascodes that isolate each stage from the next one. In the original Moog design, most of the character comes from the open-loop differential output amplifier. In this one, the differential current is converted to a voltage by a simple resistor and remains uncorrected. It behaves not so different from a diode clipping stage, just a bit smoother. As mentioned before and shown in the plot above: it starts distorting around 25mV and 90% of the maximum amplitude is reached at 75mV. I donít think itís a coincidence that these match the levels at which the oscillators enter the VCF in a Minimoog: one 25mV and all three together 75mV. But now that the brakes are off, by using an output amplifier that can handle much stronger signals, there is no need for this limitation, much higher input amplitudes can be used and these give access to a secondary filtering effect. The available charge or discharge current, for the filterís capacitors, which sets the corner frequency decreases at higher input amplitudes. This can be seen in the plot below that shows the derivative of this current. And interestingly enough, both sides of this curve approach an exponential when input amplitude is increased further, which is visible in this log-plot. This means that next to the frequency control voltage, which is exponentially converted to the control current, the filter gets a second exponential control voltage, namely the input signal itself. The above Bode magnitude plot shows how the filterís slope changes with increasing signal amplitude. In other words it becomes self-frequency-modulating at higher amplitudes. This self-modulation has as effect that when the filter is self-oscillating, the frequency at which it does this gets spread with increasing input signal. This can be seen in the scope image above where the self-oscillation is spread into 4-different frequencies depending on the voltage of the input signal at that moment. Audibly this translates in the self-oscillation sinewave being progressively blended with the input signal as its level increases until it becomes an integral part of its timbre instead of sitting on top as a whistle. Another way to describe this is frequency dependent distortion, because as long as the available charge (or discharge) current is enough for the filter capacitors to follow the slew-rate of the signal at that amplitude, the top transistors can do their job as error-correctors and distortion is absent. Note that this distortion is asymmetric as only the leading edges of the waveforms are affected and itís self-contained because it happens Ďiní the filter. Too low frequencies wonít generate extra harmonics because they are passed undistorted, too high ones are filtered out. I find this kind of behavior, where each note takes its own part of the spectrum instead of swamping everything, especially suitable for poly-synths. Now, as this filterís whole sonic behavior depends on the input signal, it seems rather pointless to use it in a Juno-106 because its input level of the filter is non-adjustable. But, I used a trick here with the Q-compensation. This has as function to keep input signal amplitude constant when resonance is increased. Without it, it gets attenuated by 14dB when the filter starts self-oscillating. Read: the resonance fader can be used as filter input level control if there is no Q-compensation. However, Q-compensation is mandatory here as I was not willing to sacrifice low-end. So, I moved the Q-compensation outside of the filterís resonance loop. By doing this, resonance still attenuates the filterís input level but at the output it remains constant. Note that from a noise perspective, this is really bad design, but here it is ok because the input signals are much stronger than in the original Juno filter, so relatively the noise is less pronounced and it is also swamped out by the rest of the Junoís noisy character. I could actually remove the stack of bandgap references without noise-compromise here and only keep the top one to keep out the junk on the supply lines. Good idea for a stand-alone design, but adding 30 of them in a synth was a bit of overkill. I also redistributed the Juno-106ís available headroom. Resonance level (the amplitude at which the filter self-oscillates) has been reduced to make room for more emphasis (how much prominence is given to certain harmonics present in the waveforms by resonance at their frequency) and to allow full Q-compensation instead of half, which translates in overall more low-end. Resonance level is now also more controllable. It starts at position 5 and gradually increases after that instead of the almost all-or-nothing around position 9 of the original. Signal levels were adjusted so that each individual one can pass the filter undistorted. Multiple ones together are distorted. To still be able to get all waveforms together undistorted, I increased the filterís frequency range to about 100kHz. When a bit of resonance is added with the filter fully open, it attenuates the input signal a bit so that it distorts less and for all frequencies of interest, this bit of resonance also acts as global negative feedback that cancels out the remaining distortion. Finally I increased the overall frequency tracking. Now it stays completely flat between 5Hz and 10kHz, as in: I cannot even measure the error and the only ripple I see comes from the nonlinearities of the DAC I used. This might sound like overkill, but it is very meaningful if you get multiple voices beating against each other: Slow evolving drones instead of the restless vibrato of the original filters. Above are 2 plots that show the pitch error vs frequency. One in pct and the other in cents. The red curve above and beyond show the Just Noticeable Difference in pitch of what humans can perceive. Anything in between is perceived as being perfectly in tune. InstallationInstallation involves the same as replacing the original 80017A chips: Desolder the original ones, Solder the AR80017A-GS ones instead and do the adjustment procedure. Adjustment procedure is the same as per service manual instructions, except 2 voltages need to be done at half the level instructed. Download adjustment changes here Copyright © Cask Strength Electronics 2025 |